Otras utilidades

Al tratarse de lenguajes de programación, el uso de R y Python no se limita únicamente al análisis estadístico. Aunque R se especializa en ello y Python es un lenguaje más amplio; también podemos utilizarlos para otros tipo de usos. A continuación te presentamos algunos de ellos.

Creación de programas informáticos

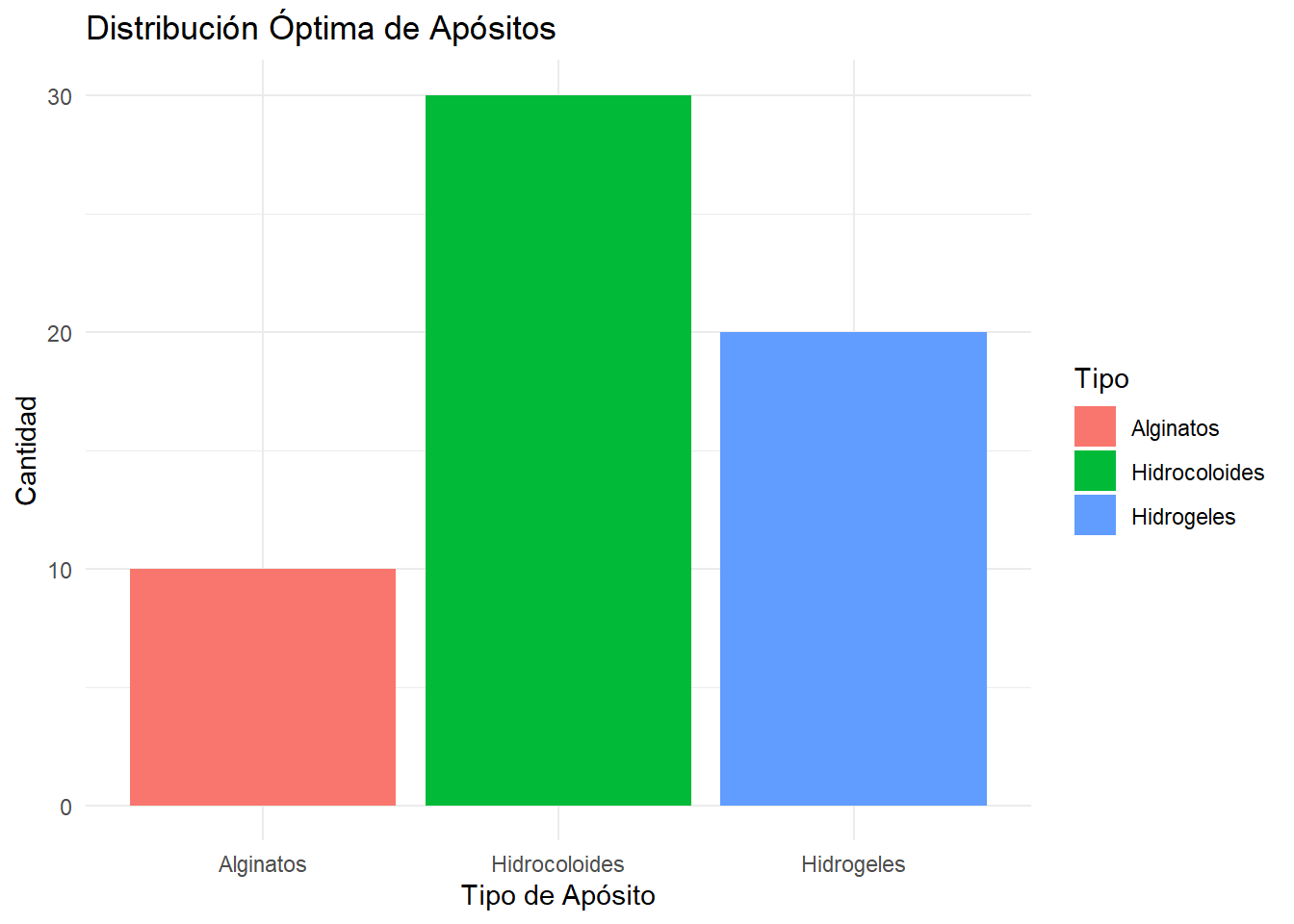
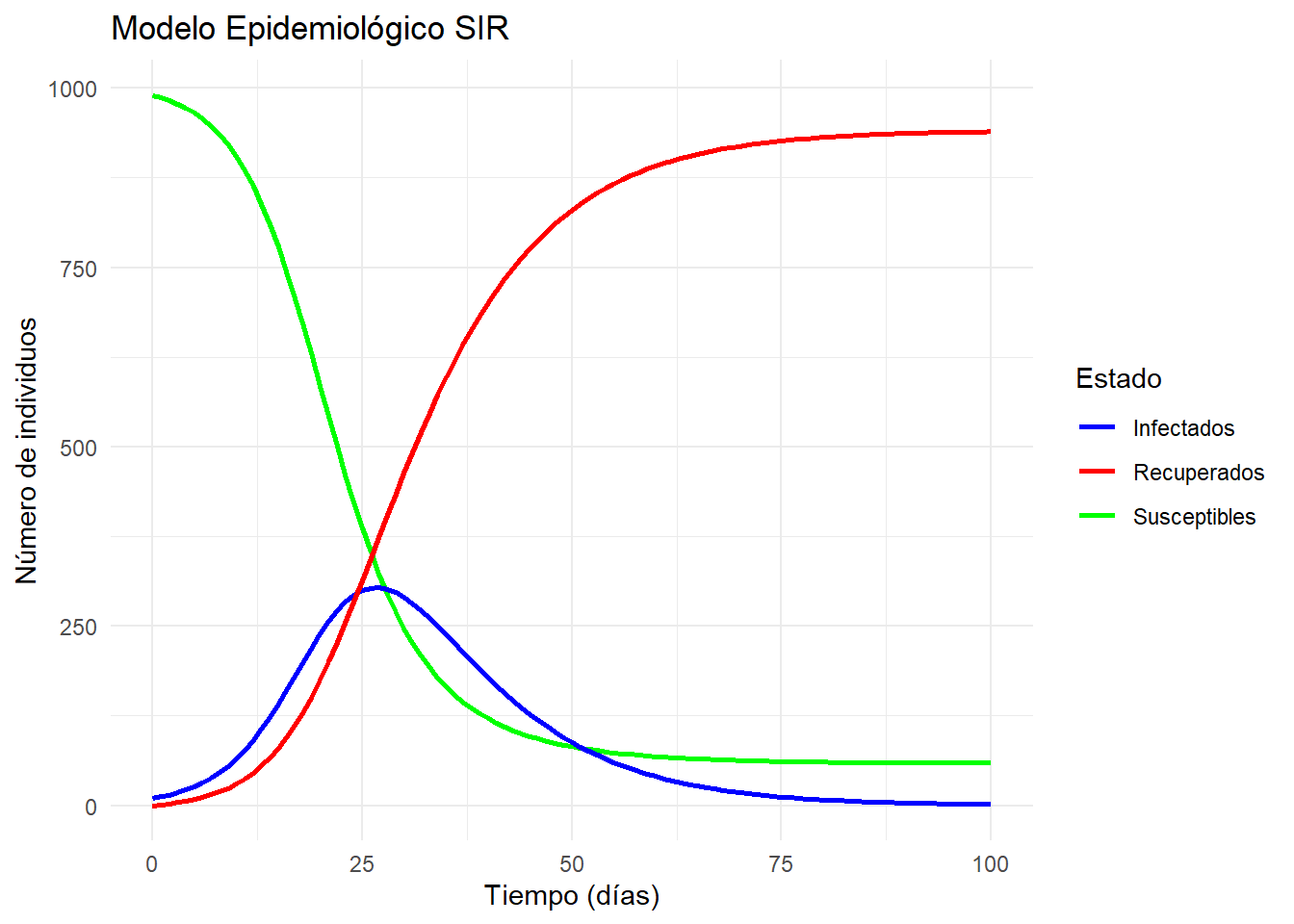
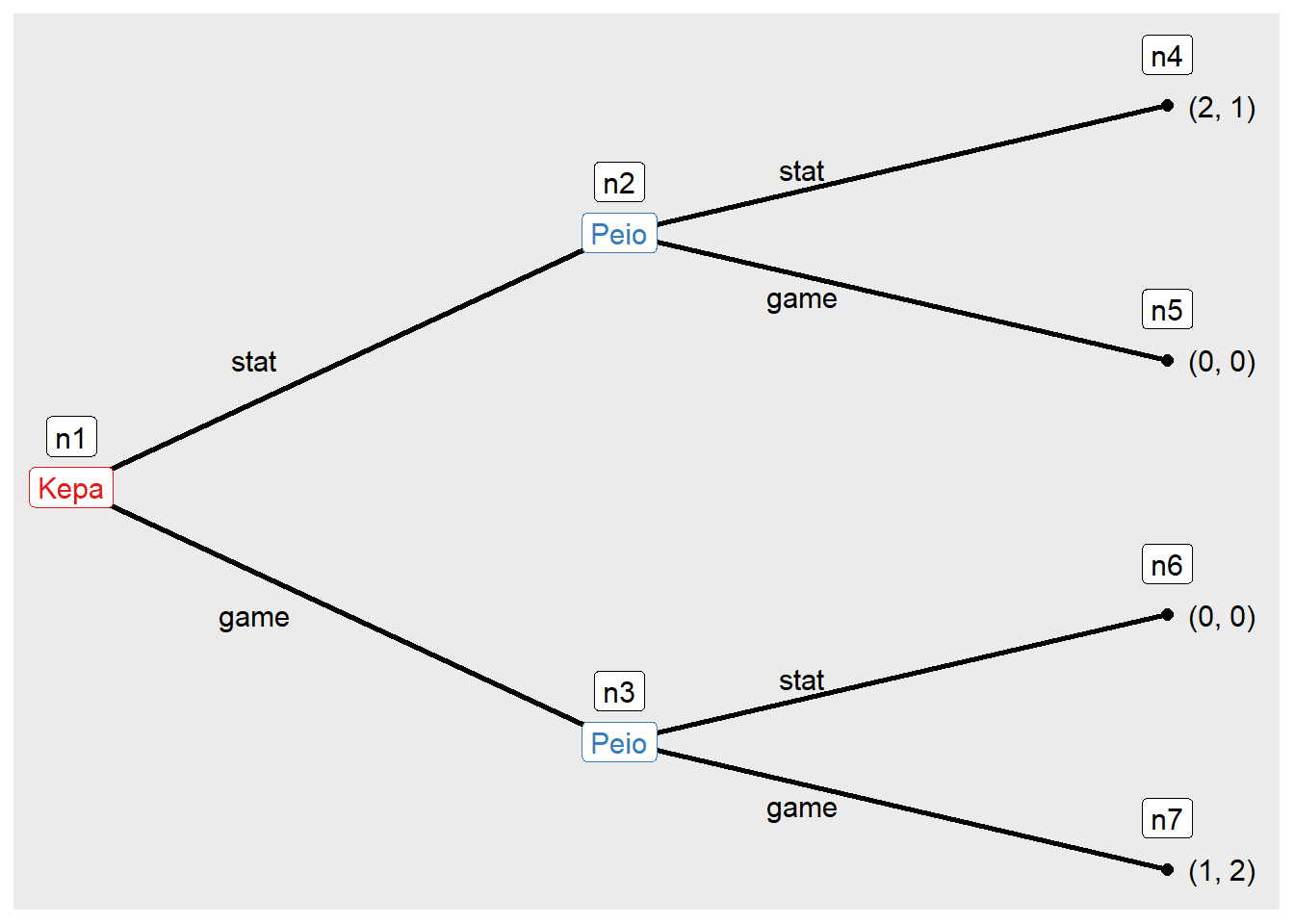
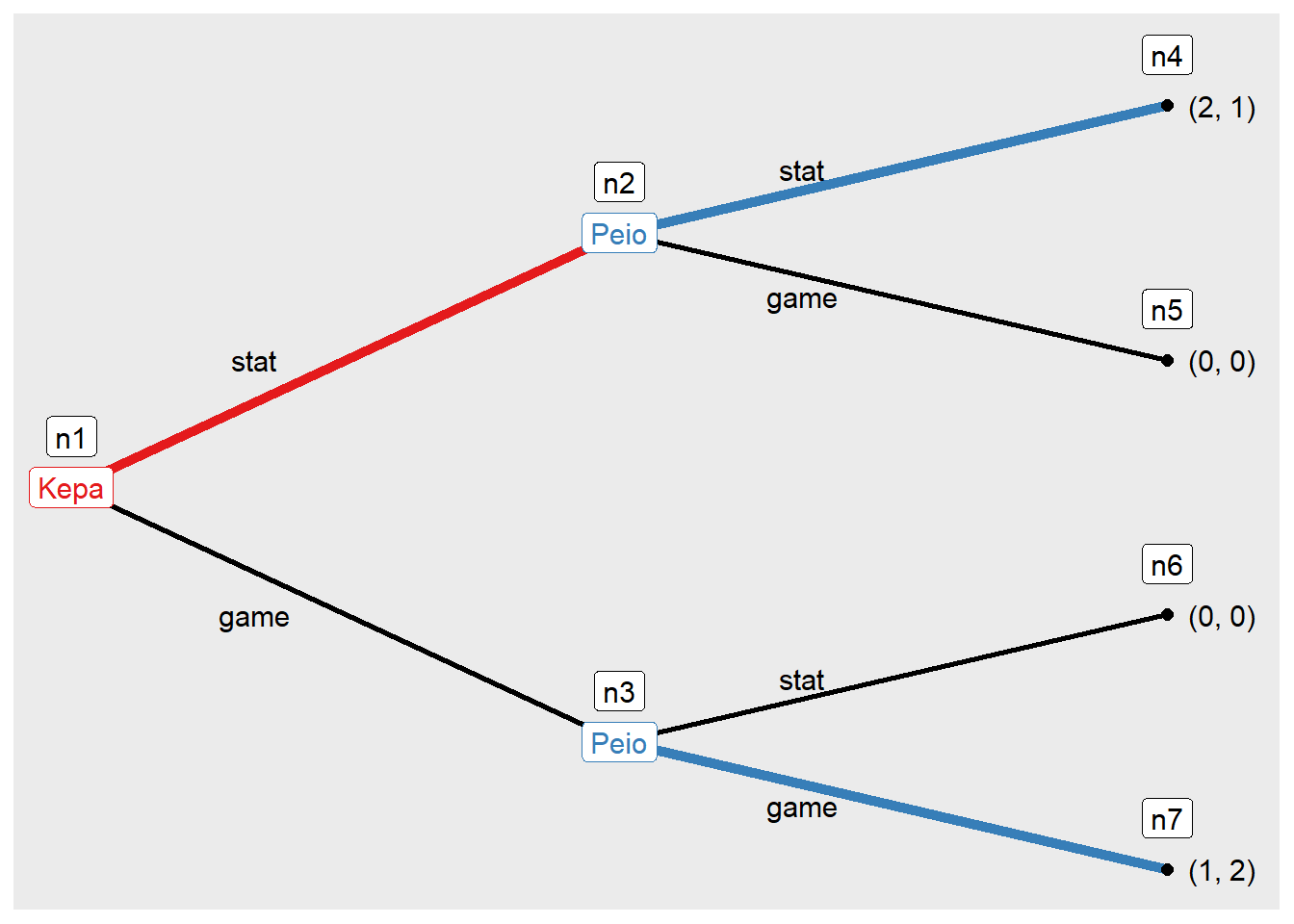
Ambos lenguajes pueden ser utilizados para la creación de programas informáticos debido a que pueden integrar otro tipo de lenguajes como son html, JavaScript y CSS. Para poder hacerlos hacemos uso de Frameworks:

Un framework de desarrollo web es una estructura o conjunto de herramientas predefinidas que proporciona una base para la construcción de aplicaciones web

Nosotros os presentamos dos de ellos: shiny y djando (este último ha sido utilizado para la creación de aplicaciones tan famosas como Spotify o Instagram).

---

Ejemplo de una app

A continuación os presentamos un pequeño ejemplo de una app realizada con shiny. Se trata de la escala de Braden:

#| '!! shinylive warning !!': |
#|   shinylive does not work in self-contained HTML documents.
#|   Please set `embed-resources: false` in your metadata.
#| standalone: true
#| viewerHeight: 1000
library(shiny); library(shinyWidgets); library(bslib); library(dplyr)

ui <- fluidPage(theme = bs_theme(preset = "shiny"),
                br(),
                h3("Escala de Braden"),
                hr(),
                wellPanel(radioGroupButtons(
                    inputId = "Sensorial",
                    label = "Percepción sensorial",
                    choices = c("Completamente limitada", "Muy limitada", "Ligeramente limitada","Sin limitaciones"),
                    direction = "horizontal",
                    justified = T
                  ),
                  radioGroupButtons(inputId = "Humedad",
                                    label = "Exposición a al humedad",
                                    choices = c("Constantemente húmeda", "Húmeda con frecuencia", "Ocasionalmente húmeda","Raramente húmeda"),
                                    direction = "horizontal",
                                    justified = T
                  ),radioGroupButtons(inputId = "Actividad",
                                      label = "Actividad",
                                      choices = c("Encamado", "En silla", "Deambula ocasionalmente","Deambula frecuentemente"),
                                      direction = "horizontal",
                                      justified = T
                  ),
                  radioGroupButtons(inputId = "Movilidad",
                                    label = "Movilidad",
                                    choices = c("Completamente inmovil", "Muy limitada", "Ligeramente limitada","Sin limitaciones"),
                                    direction = "horizontal",
                                    justified = T
                  ),
                  radioGroupButtons(inputId = "Nutricion",
                                    label = "Nutrición",
                                    choices = c("Muy pobre", "Probablemente inadecuada", "Adecuada","Excelente"),
                                    direction = "horizontal",
                                    justified = T
                  ),
                  radioGroupButtons(inputId = "Riesgo_lesion",
                                    label = "Riesgo de lesiones cutáneas",
                                    choices = c("Problema", "Problema potencial", "No existe problema aparente"),
                                    direction = "horizontal",
                                    justified = T
                  )
                ),
                  br(),
                    wellPanel(
                      h4("Resultado"),
                      fluidRow(
                        column(6,h6("Resultado numérico"),
                               verbatimTextOutput("resultado")),
                        column(6,h6("Interpretación"),
                               uiOutput("interpretacion"))
                      )
                    )
                  )

server <- function(input,output,session){
  suma <- reactiveVal(0)
  observe({
    sensorial <- if_else(input$Sensorial == "Completamente limitada",1,
                         if_else(input$Sensorial == "Muy limitada",2,
                                 if_else(input$Sensorial == "Ligeramente limitada",3,4)))
    humedad <- if_else(input$Humedad == "Constantemente húmeda",1,
                       if_else(input$Humedad == "Húmeda con frecuencia",2,
                               if_else(input$Humedad == "Ocasionalmente húmeda",3,4)))
    actividad <- if_else(input$Actividad == "Encamado",1,
                         if_else(input$Actividad == "En silla",2,
                                 if_else(input$Actividad == "Deambula ocasionalmente",3,4)))
    movilidad <- if_else(input$Movilidad == "Completamente inmovil",1,
                         if_else(input$Movilidad == "Muy limitada",2,
                                 if_else(input$Movilidad == "Ligeramente limitada",3,4)))
    nutricion <- if_else(input$Nutricion == "Muy pobre",1,
                         if_else(input$Nutricion == "Probablemente inadecuada",2,
                                 if_else(input$Nutricion == "Adecuada",3,4)))
    lesion <- if_else(input$Riesgo_lesion == "Problema",1,
                      if_else(input$Riesgo_lesion == "Problema potencial",2,3))
    valor = sensorial + humedad + actividad + movilidad + nutricion + lesion
    suma(valor)
  })
  output$resultado <- renderText({
    suma()
  })
  output$interpretacion <- renderUI({
    valor <- suma()
    inter <- if_else(valor < 12, "Riesgo alto",
                     if_else(valor <= 15, "Riesgo medio",
                             if_else(valor <= 18,"Riesgo bajo","Sin riesgo")))
    if (grepl("Riesgo alto", inter)) { # Si contiene "riesgobajo"
      tags$pre(style = "color: red; font-weight: bold;", inter )
    } else {
      if (grepl("Riesgo medio", inter)) { # Si contiene "riesgobajo"
        tags$pre(style = "color: orange; font-weight: bold;", inter )
      } else {
        if (grepl("Riesgo bajo", inter)) { # Si contiene "riesgobajo"
          tags$pre(style = "color: #acaa0e; font-weight: bold;", inter )
        } else {
          if (grepl("Sin riesgo", inter)) { # Si contiene "riesgobajo"
            tags$pre(style = "color: green; font-weight: bold;", inter )
          }}}}
  })
  
}

shinyApp(ui,server)

---

Problemas lógicos y de optimización

Otra utilidad que os presentamos es el uso de nuestros lenguajes de programación para tratar con problemas de optimización; problemas tan acuciantes en Osakidetza. Podemos hacer uso de librerías especializadas en tratar con estos problemas para solucionar distintas situaciones. A continuación os presentamos un ejemplo en R y Python:

Realizado en R

Enunciado

En un hospital, las enfermeras deben seleccionar los apósitos adecuados para tratar úlceras por presión en los pacientes. El hospital dispone de tres tipos de apósitos: hidrocoloides, hidrogeles y alginatos. Cada tipo de apósito tiene un costo asociado por unidad, y existen requerimientos mínimos de uso para garantizar una atención adecuada a los pacientes. Además, el hospital cuenta con una capacidad máxima disponible para cada tipo de apósito debido a restricciones presupuestarias y de inventario.

Datos del problema: Costos por unidad:

- Hidrocoloides: 10 €/unidad

- Hidrogeles: 15 €/unidad

- Alginatos: 25 €/unidad

Requerimientos mínimos:

- Se necesitan al menos 30 unidades de hidrocoloides.

- Se necesitan al menos 20 unidades de hidrogeles.

- Se necesitan al menos 10 unidades de alginatos.

Capacidades máximas disponibles:

- Hidrocoloides: hasta 50 unidades.

- Hidrogeles: hasta 40 unidades.

- Alginatos: hasta 30 unidades.

Objetivo: Determinar la cantidad óptima de cada tipo de apósito que debe utilizarse para minimizar el costo total, cumpliendo con los requerimientos mínimos y respetando las capacidades máximas disponibles.

Pregunta: ¿Cuántas unidades de cada tipo de apósito deben usarse para minimizar el costo total del tratamiento? ¿Cuál será el costo mínimo total?

library(lpSolve)

# ============================================
# 1. Definición del problema
# ============================================

# Costos por unidad de cada tipo de apósito
costos <- c(10, 15, 25)  # Hidrocoloides, Hidrogeles, Alginatos

# Restricciones (requerimientos mínimos para los pacientes)
requerimientos <- c(30, 20, 10)  # Cantidad mínima necesaria de cada tipo de apósito

# Capacidad máxima disponible para cada tipo de apósito
capacidades <- c(50, 40, 30)

# Matriz de restricciones (filas: tipos de apósitos; columnas: variables)
matriz_restricciones <- rbind(
  c(1, 0, 0), # Restricción para hidrocoloides
  c(0, 1, 0), # Restricción para hidrogeles
  c(0, 0, 1)  # Restricción para alginatos
)

# Tipos de restricción (>= para requerimientos mínimos)
direcciones <- rep(">=", length(requerimientos))

# ============================================
# 2. Resolver el problema con lpSolve
# ============================================

resultado <- lp(
  direction = "min",                # Minimizar el costo total
  objective.in = costos,            # Función objetivo (costos)
  const.mat = matriz_restricciones, # Matriz de restricciones
  const.dir = direcciones,          # Tipos de restricciones (>=)
  const.rhs = requerimientos        # Lado derecho (requerimientos mínimos)
)

# ============================================
# 3. Mostrar los resultados
# ============================================

cat("Costo mínimo total:", resultado$objval, "\n")

Costo mínimo total: 850 

cat("Cantidad óptima de apósitos:\n")

Cantidad óptima de apósitos:

names(resultado$solution) <- c("Hidrocoloides", "Hidrogeles", "Alginatos")
print(resultado$solution)

Hidrocoloides    Hidrogeles     Alginatos 
           30            20            10 

# ============================================
# Visualización gráfica del resultado
# ============================================

library(ggplot2)

df_resultados <- data.frame(
  Tipo = c("Hidrocoloides", "Hidrogeles", "Alginatos"),
  Cantidad = resultado$solution
)

ggplot(df_resultados, aes(x = Tipo, y = Cantidad, fill = Tipo)) +
  geom_bar(stat = "identity") +
  labs(title = "Distribución Óptima de Apósitos",
       x = "Tipo de Apósito",
       y = "Cantidad") +
  theme_minimal()

Realizado en Python

Enunciado:

Un hospital tiene tres tipos de turnos: mañana, tarde y noche. Para cada turno, se requieren un número mínimo de enfermeras para garantizar la atención adecuada de los pacientes. Cada tipo de enfermera tiene un costo diferente por hora.

Los datos del problema son los siguientes:

Turnos: Mañana, Tarde y Noche.

Requerimiento mínimo de enfermeras:

Mañana: 5 enfermeras

Tarde: 4 enfermeras

Noche: 3 enfermeras

Costos por hora:

Enfermeras para turno de mañana: 10 €/hora

Enfermeras para turno de tarde: 12 €/hora

Enfermeras para turno de noche: 15 €/hora

Objetivo: Determinar la cantidad de enfermeras a asignar a cada turno de forma que se minimicen los costos totales, cumpliendo con los requerimientos mínimos de personal para cada turno.

from pulp import LpProblem, LpMinimize, LpVariable, LpStatus, SCIP_PY

# Crear el problema de optimización
prob = LpProblem("Minimizar_Costos_Enfermeras", LpMinimize)

# Definir las variables de decisión (cantidad de enfermeras asignadas a cada turno)
x1 = LpVariable('x1', lowBound=5, cat='Integer')  # Enfermeras para turno de mañana
x2 = LpVariable('x2', lowBound=4, cat='Integer')  # Enfermeras para turno de tarde
x3 = LpVariable('x3', lowBound=3, cat='Integer')  # Enfermeras para turno de noche

# Definir la función objetivo (minimizar el costo total)
prob += 10 * x1 + 12 * x2 + 15 * x3, "Costo Total"

# Resolver el problema utilizando CBC (COIN-OR CBC)
prob.solve(SCIP_PY(msg=True))

1

# Mostrar el resultado
if prob.status == 1:
    print(f"Cantidad de enfermeras para turno de mañana: {x1.varValue} enfermeras")
    print(f"Cantidad de enfermeras para turno de tarde: {x2.varValue} enfermeras")
    print(f"Cantidad de enfermeras para turno de noche: {x3.varValue} enfermeras")
    print(f"Costo total mínimo: {prob.objective.value()} €")
else:
    print(f"El problema no tiene solución óptima. Estado: {LpStatus[prob.status]}")

Cantidad de enfermeras para turno de mañana: 5.0 enfermeras
Cantidad de enfermeras para turno de tarde: 4.0 enfermeras
Cantidad de enfermeras para turno de noche: 3.0 enfermeras
Costo total mínimo: 143.0 €

---

Ecuaciones diferenciales y modelos epidemiológicos

Nuestros lenguajes de programación también son usado para la realización de vigilancia y modelaje epidemiológico a través de modelos como SIR y SEIR.

A continuación presentamos un ejemplo de su uso:

Enunciado

Un hospital desea modelar la propagación de una enfermedad infecciosa en una población cerrada de 1,000 individuos. La enfermedad se transmite de persona a persona con una tasa de transmisión del 30% por contacto entre un individuo susceptible y uno infectado. Además, los individuos infectados se recuperan a una tasa del 10% por día, es decir, el tiempo promedio para que una persona se recupere es de 10 días.

Inicialmente, hay 990 personas susceptibles, 10 personas infectadas y ninguna persona recuperada. El objetivo es analizar cómo evoluciona la propagación de la enfermedad a lo largo de 100 días y determinar:

1. ¿Cuándo alcanza la enfermedad su pico máximo de infectados?

2. ¿Cuántas personas permanecen susceptibles al final del período?

3. ¿Cuántas personas se habrán recuperado después de 100 días?

# ============================================
# Modelo Epidemiológico SIR en R
# ============================================

# Instalar y cargar el paquete necesario
library(deSolve)

# ============================================
# 1. Definir el modelo SIR
# ============================================

sir_model <- function(time, state, parameters) {
  with(as.list(c(state, parameters)), {
    # Ecuaciones diferenciales del modelo SIR
    dS <- -beta * S * I / N         # Cambio en la población susceptible
    dI <- beta * S * I / N - gamma * I # Cambio en la población infectada
    dR <- gamma * I                # Cambio en la población recuperada
    
    # Retornar las derivadas
    return(list(c(dS, dI, dR)))
  })
}

# ============================================
# 2. Parámetros y condiciones iniciales
# ============================================

# Parámetros del modelo
parameters <- c(
  beta = 0.3,   # Tasa de transmisión (probabilidad de contagio por contacto)
  gamma = 0.1   # Tasa de recuperación (1/duración promedio de la enfermedad)
)

# Condiciones iniciales
initial_state <- c(
  S = 990,  # Población susceptible inicial
  I = 10,   # Población infectada inicial
  R = 0     # Población recuperada inicial
)

# Tamaño total de la población
N <- sum(initial_state)

# Tiempo de simulación (en días)
time <- seq(0, 100, by = 1)

# ============================================
# 3. Resolver el sistema de ecuaciones diferenciales
# ============================================

output <- ode(
  y = initial_state,
  times = time,
  func = sir_model,
  parms = parameters
)

# Convertir el resultado a un dataframe para facilitar la visualización
output_df <- as.data.frame(output)

# ============================================
# 4. Visualización de los resultados
# ============================================

library(ggplot2)

ggplot(data = output_df, aes(x = time)) +
  geom_line(aes(y = S, color = "Susceptibles"), size = 1) +
  geom_line(aes(y = I, color = "Infectados"), size = 1) +
  geom_line(aes(y = R, color = "Recuperados"), size = 1) +
  labs(
    title = "Modelo Epidemiológico SIR",
    x = "Tiempo (días)",
    y = "Número de individuos",
    color = "Estado"
  ) +
  theme_minimal() +
  scale_color_manual(values = c("blue", "red", "green"))

---

Mapas interactivos

Nuestros lenguajes de programación también disponen de formas para crear gráficos y mapas interactivos. Una gran utilidad puede ser la creación de mapas geoespaciales interactivos del que os dejamos un pequeño ejemplo:

# Cargar la librería leaflet
library(leaflet)

# Crear un mapa centrado en Madrid, España
mapa <- leaflet() %>%
  setView(lng = -3.7038, lat = 40.4168, zoom = 12) %>%
  addTiles()

# Añadir marcadores para algunos puntos de interés
mapa <- mapa %>%
  addMarkers(lng = -3.7038, lat = 40.4168, popup = "Puerta del Sol") %>%
  addMarkers(lng = -3.6934, lat = 40.4180, popup = "Museo del Prado") %>%
  addMarkers(lng = -3.6887, lat = 40.4076, popup = "Parque del Retiro")

# Añadir un círculo alrededor del centro de la ciudad
mapa <- mapa %>%
  addCircles(lng = -3.7038, lat = 40.4168, radius = 1000, color = "red", fillColor = "pink")

# Añadir una capa de polígono para representar un área
area_poligono <- data.frame(lng = c(-3.71, -3.69, -3.68, -3.70),
                            lat = c(40.41, 40.42, 40.41, 40.40))


# Mostrar el mapa
mapa

---

Teoría de juegos

Otro ejemplo de los distintos usos que tienen nuestros lenguajes de programación sería para resolver problemas relacionadas con teoría de juegos. A continuación os presentamos un ejemplo:

library(rgamer)

# Definimos el juego

juego <- extensive_form(
  players = list("Kepa", 
                 rep("Peio", 2),
                 rep(NA, 4)),
  actions = list(c("stat", "game"),
                  c("stat", "game"), c("stat", "game")),
  payoffs = list(Kepa = c(2, 0, 0, 1),
                 Peio = c(1, 0, 0, 2)),
  direction = "right")

solucion_juego <- solve_efg(juego)

backward induction: [(stat), (stat, game)]

show_path(solucion_juego)